Analytic pluck synthesis

Geraint Luff

2021-03-21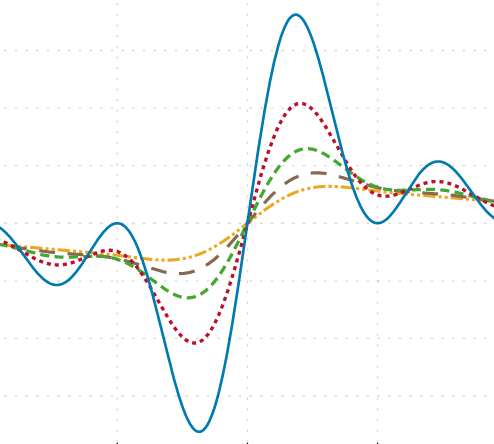 original

No feedback, no wavetables, no aliasing: synthesising a plucked-string sound using a family of directly-computable band-limited impulses.

Background

This article assumes you're familiar with Fourier analysis, complex phase and aliasing.

Here's something cool I found: a family of band-limited impulses where each frequency decays exponentially as we increase the shape parameter:

I've called this family of curves BLEX due to their exponentially-decaying spectra. Their equation and frequency-response are below.

When used as an impulse train, this means we can synthesise a plucked-string sound with no aliasing, no detuning/phase issues, and no delay-buffers. Let's look at how that works:

Plucked strings

The key property which makes an instrument sound "plucked" is exponential decay. To sound natural, each harmonic decays at a different rate (usually faster for higher harmonics):

Amplitudes of harmonics in a synthesised pluck over time. You can see the higher-pitched harmonics die away much earlier than the 220Hz fundamental, making the sound increasingly mellow.

A common method for synthesising decaying harmonics like this is Karplus-Strong, which tunes a feedback-delay loop to the period of our virtual resonator/string, and sends an impulse through it to make it go "ding":

A big challenge with Karplus-Strong is choosing the delay to put inside the loop, because the ideal delay has some conflicting requirements:

support fractional delays (because most notes won't have whole-sample wavelengths)
have a very flat amplitude response (otherwise long notes will decay faster than intended)
be linear phase (otherwise some frequencies are delayed longer than others, so harmonics can end up out of tune)
support small delay times (for high notes)

Balancing these goals is tricky - on the other hand the overall structure is simple and intuitive, and you can get quite creative with the decay filter.

But we're not here for Karplus-Strong, let's try something different!

The exponential-frequency click

Here's a neat family of pulse signals:

f_k(x) = \frac{k}{k^2 + (2 \pi x)^2}

They're interesting because their Fourier transforms decay exponentially, with both increasing frequency \omega and the parameter k:

F_k(\omega) = e^{-k |\omega|}

Each curve decreases exponentially as |\omega| increases, but each frequency also decays exponentially as we increase k.

Impulse train

If you repeat an impulse at regular intervals, you get a periodic signal (i.e. a note) with a timbre/spectrum derived from the impulse:

So, what happens if we repeat our pulses, but increasing k linearly with time? We get a note where each harmonic fades away exponentially at a different rate:

You can see the impulses changing shape as the note progresses

Awesome - except we clearly have some DC offset, because our pulses all have DC offset. What can we do about that?

90° phase shift

Even-symmetric impulses often have problems with DC offset - but if you shift the phase of each frequency by 90 degrees, you get an odd-symmetric impulse. There's a neat equation for this variant as well:

g_k(x) = \frac{2 \pi x}{k^2 + (2 \pi x)^2}

No DC offset — plus, it just *looks* prettier. 😛

The spectrum still decays exponentially in k and \omega, but it's entirely imaginary, and the positive/negative halves are flipped:

\DeclareMathOperator{\sgn}{sgn} G_k(\omega) = -e^{-k |\omega|} \sgn(\omega)

The amplitude of every frequency is preserved (aside from the DC offset). Let's see what that looks like:

Aliasing

These impulses are cool, but they contain frequencies way above Nyquist. That means we get aliasing, particularly for smaller k. Here's the spectrum of a note (made from k=5 impulses) where the aliasing is, uh... visible:

We can see the harmonics we want slowly decaying at the top - but with higher harmonics aliased down in between them.

Band-limited variant

What would be great is a band-limited version of the these impulses. We want them to have the same exponential shape as before up to Nyquist, and then suddenly disappear, like this:

It turns out there's a computable time-domain solution for this:

\frac{2 \pi x - e^{-k/2}\left( k \cdot \sin(\pi x) + 2 \pi x \cdot \cos(\pi x) \right)}{k^2 + (2 \pi x)^2}

Don't ask how I found this - if I confess to it they'll revoke my maths degree.

Higher values of k wobble around less, corresponding to a smaller jump when the spectrum cuts off at Nyquist

The equation's a bit messier than our previous version, and not quite as simple to evaluate. Unlike the non-bandlimited version, this is defined and bounded for all real k, although we still need a special case for x = k = 0.

Let's see what happens when we create a note from these, with linearly-increasing k as before:

This might look the same as the previous one, but it has the warm glow of nitpicky correctness.

If we use our new band-limited impulses to plot the spectrum where we previously saw the aliasing, improvements are pretty clear:

Conclusion

So there you have it! Perfectly-pitched alias-free string-plucks.

I couldn't find this mentioned anywhere else, so (following the naming convention of BLIT, BLEP and BLAMP) I've been calling this family of impulses BLEX (Band-Limited EXponential).

Because it's analytically generating the impulses, k can be trivially modulated or even reversed:

Computing the band-limited impulse seems tricky. You have \exp(), \sin() and \cos() as well as the division - and the wider your window, the more your impulses overlap.

But I think it's fun! I haven't put this in a synth yet, but maybe someone will find it useful. 🙂