Extra-wide window functions

Geraint Luff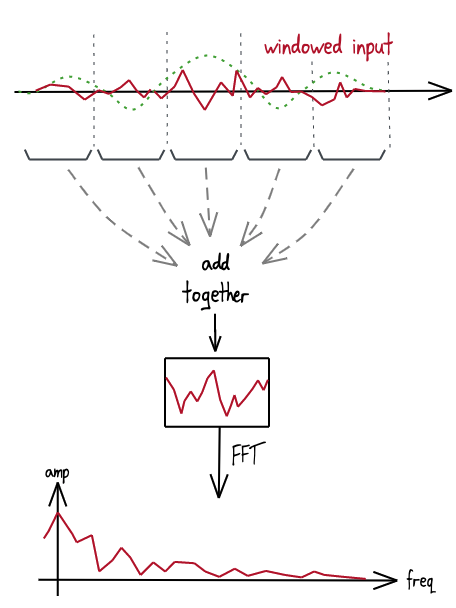

Window functions are typically matched to the length of your FFT, but they don't have to be. Let's look at how we can use a window longer than the FFT size.

Single-period windows

When performing FFT analysis, typical window functions are exactly as long as the FFT length:

Some typical windows, zero-valued outside the [0, 1] range. The time unit here is "FFT lengths".

We generally want a window function to have a narrow peak in the spectrum, and small side-lobes, but this time-domain limitation means our goals are always compromised:

spectra for some typical windows

When we multiply our input by this window, the spectrum of that input gets convolved by this window - so a perfect sine peak gets smudged into a shape which matches our Hann spectrum above:

An input sine signal, with and without a window - each spectrum is normalised so the peak is at 0dB.

The FFT doesn't compute these smooth curves - it produces the values at each (integer) bin. This means that a certain amount of spreading out the peak is useful, otherwise we could miss it completely unless it landed exactly on a bin.

But you can see that the peak is much wider than a single bin, and we also have those side-lobes which produce a long tail of inconvenient values in other bins.

Choosing the right window function is always a compromise, and to make a good choice you should understand what properties are most important for your situation.

Multi-period windows

If our window is longer than a single FFT length, we can achieve better results. Here we have sinc(t) and sinc(t)^2, both windowed with Blackman-Harris within the range ±6:

Our windows are now 12 FFT time-periods long, but this lets them have tight peaks and a quicker roll-off compared to our previous windows:

Let's look at those with linear amplitude (instead of dB), and zoom in a bit on the x-axis:

spectra for our windows, normalised so the peaks are 1

The spectra of these windows approximate a rectangular shape between ±0.5, and a triangular shape between ±1. This approximation gets better as we use wider versions of these windows.

If you consider how these windows would smudge the peaks of our spectrum, this means that a pure sine-wave peak would appear in exactly one bin (for BH-sinc) or distributed between the two nearest bins (for BH-sinc2).

That's pretty neat! 🙂

How to use multi-period windows

The FFT expects input of a particular length, so to actually use these, we first multiply by the window, and then wrap the input around into a single FFT-length block:

diagram of how to wrap/sum the input when the window function is longer than the FFT size

This wrap-around-and-sum method works because the FFT assumes a periodic signal. Or (phrased a different way), it only calculates values for frequencies which are integer multiples of the FFT length, so you can fold all the segments together to get the same result.

Drawbacks

The most obvious drawback is that the window extends past t = 1, which means we have some latency. Short sounds (transients) will also appear and disappear more gradually in our analysis, as they get caught by the wider tails of the window.

You also have to think a bit more carefully before using these windows for anything except analysis (e.g. STFT/frequency-domain processing), because the normal requirements such as the WOLA condition are no longer sufficient.

The opposite of zero-padding

Here's an alternative perspective on what we're doing.

When performing spectral analysis (e.g. for display or peak-finding), we often want to find peaks in between the bins, and an easy way to do this is add a bunch of zeros to the input, thereby taking a longer FFT for the same input:

If we extended our input infinitely in each direction, we would get a continuous spectrum. One way to understand zero-padding is sampling the "true" (continuous) spectrum more often.

We can view what we're doing here (with the extra-wide windows) as the opposite of zero-padding: sampling the continuous spectrum less often.

This means we're dropping information, because we have fewer bins. But when our window's central peak is several bins wide, that's fine - if we squished our extra-wide windows back into the [0, 1] range, their spectral peaks would be 12x wider, and we might (rightly) wonder whether we really needed the values for every bin.

Conclusion

So: FFT length and window length don't have to be linked, and if the window is longer, we wrap/sum the input back into the shorter FFT size.

This might not be useful on its own yet 🤷 - I mostly wrote this because this way of thinking about window functions lays the groundwork for some fun stuff later, including: