Stride-Interpolated Delay

Geraint Luff

2021-05-12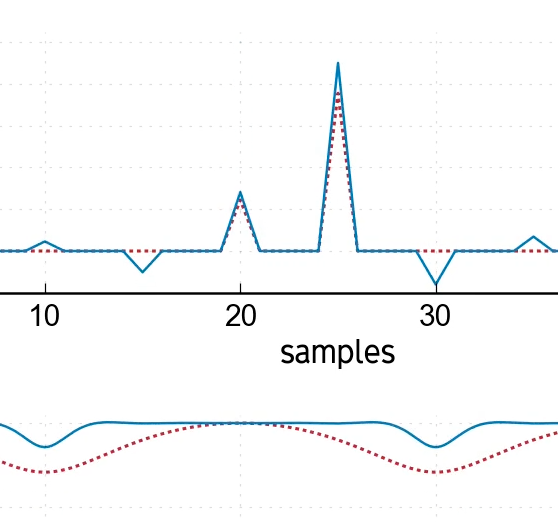 original

When we change the length of a delay-line, we usually use either a smooth slide (with detuning) or a cross-fade (with comb-filtering artefacts). Let's look at a third option!

Let's say you have a delay line, where you're writing into a buffer, and reading out from a previous position in the buffer:

We want to somehow transition to a new delay length:

We look at a couple of ways to go about this, and then explore a (slightly quirkier) third approach.

Typical approaches

There are generally two solutions to this problem:

1. Smoothly slide the delay time
2. Fade between two distinct delay times

Let's consider both options in terms of a dynamically-changing impulse response, and look at the frequency-domain implications.

For all of the illustrations below, we're going to transition between a 20-sample delay and a 25-sample delay.

Smoothly sliding the delay time

Here, we have a single delay tap, which smoothly varies between the two lengths.

Even if the start/end delays are an integer number of samples, the intermediate delays won't be - so we need a fractional delay:

Here we've used 10-point windowed-sinc interpolation (Lanczos), and you can see the impulse response shifting around to produce the fractional delay. The frequency response shifts with it, but it's mostly flat and smooth aside from the top end.

For comparison, we've also included linear interpolation, where the frequency response is much less consistent.

Modulation / aliasing

As delay-time moves, the shifting frequency-response ends up modulating certain frequencies (both in amplitude, and with an uneven phase response). When this happens quickly, it can produce ugly artefacts, spreading those frequencies out across other parts of the spectrum.

This clearly shows the benefits of high-quality interpolation methods when changing delay-length. It's not just that the responses are flat, but they are more consistent for different fractional delays, meaning you don't accidentally modulate parts of the signal.

Detuning

This method will also detune the input. On the plots, each frequency is constantly shifting phase (with higher frequencies moving faster), which ends up shifting that frequency up or down in the output.

If you're deliberately modulating the delay line (e.g. in a chorus effect), you want this detuning! But in other cases, you don't, and the detuning is a problem - often tackled by limiting how fast the delay-time can change.

Fading between delay-times

This method is simple to implement, particularly if your delay lengths are always integers. You compute the output for both delay lengths, and fade from the old one to the new one:

The phases stay mostly stable, so we avoid the detuning. Unfortunately, during the fade we have a comb pattern in the frequency response, which can colour the sound.

If this only happens occasionally (e.g. when the user explicitly moves a dial), it could be fine - but if the delay time is constantly shifting, you'll constantly have these comb-filter artefacts.

Stride-interpolated delay

So here's the idea: as well as the start/end delay times, we calculate some additional delay times before and after this (with the same spacing, or "stride").

We then use these to shift between the delay times - like a fractional delay, but instead of using adjacent samples, the delay taps are spaced-out:

We still get a comb-filter pattern, just as the fade did - but the notches are noticeably narrower! The better our interpolation scheme, the narrower these notches become.

And much like the "fade" method, the frequencies don't shift phase very much, so we won't get much detuning.

Drawbacks and limitations

Phase smearing

One possible issue is that the phase response has some sharper corners, corresponding to a less consistent group delay. This corresponds to a more spread-out impulse response, which could produce a diffuse/smeared sound during the transition (although this depends how far apart the old/new delay times are).

Large jumps

Another problem is that our stride has to be of limited size, otherwise we could end up trying to read future samples. One solution is to fall back to a worse interpolation method (e.g. linear) for larger changes, using this method only for smaller/gradual changes. This would also limit the impact of the phase-smearing mentioned above.

Links to the other methods

A different solution to the above large-jump issue would be to perform a series of faster, smaller transitions. When taken to its extreme, this becomes the "slide" method.

We can also interpret the "fade" method as an instance of stride-interpolated delay, just using linear-interpolation. The wider notches in the comb-filter pattern correspond to linear interpolation's uneven fractional-delay response.

When might this be useful?

I came up with this approach while considering how to modulate the pitch of a Karplus-Strong resonator (i.e. a high-feedback delay loop short enough to produce a note). This is usually changed using the "slide" method (to avoid comb-filter artefacts), but I was curious if there was a different way to do it.

But there are more practical applications: I once had a tricky problem with a tempo-synced delay, where when I automated the tempo, it detuned all the echoes as the delay-times shifted. But the tempo changed slowly throughout the whole track, so the standard alternative (fading) produced comb-filter artefacts.

Neither of the typical solutions deal well with constant small changes like this. Being able to transition delay times without comb-filter colouration or significant detuning is quite an appealing idea.

What next?

I haven't put this in an effect yet - the first step was to make sure the maths is sound. This has so far been a few sketches on bits of paper, and it's dead satisfying when the graphs come out looking exactly as I hoped/expected.

The plots above were based on a (rough) C++ implementation, and I might release that in case it's interesting/helpful for anyone else.

But for now, I'm going to stare some more at those hypnotically undulating graphs...